Tessellation

There are two parts to Tessellation Planning: the first is the use of tessellation geometry to create a layout plan. The second is to do with the design of housing layout to sreate neighbourhoods. This site explains the first.

To decorate a large surface, it is easier to use a repeating pattern rather than a haphazard non-repeating one. It would often look more beatifull too.
Any repeating pattern of shapes that cover a plane without overlap is considered a tessellation. Tiling is the simplest form tessellations.

In Latin, "tessella" was a small cubical piece of clay, stone or glass used to make mosaics. The word "tessella" also means "small square" (from "tessera", square, which in its turn is from the Greek word for "four"). They were used to make up 'tessellata' - the mosaic pictures forming floors and tilings in Roman buildings.

For example, the Islamic religion forbids the representation of living objects in works of art. The Moors have consequently created only abstract geometrical works composed of simple shapes. Nevertheless, their works of intricate design are nothing short of breathtaking. On the other hand, Romans and other Mediterranean peoples have incorporated detailed illustrations of humans and natural scenes into their designs.

In mathematics, to tessellate means to cover a plane with a pattern without gaps or
overlap. A regular polygon has 3 or 4 or 5 or more sides and angles, all equal. A regular tessellation means a tessellation made up of congruent regular polygons. Regular means that the sides of the polygon are all the same length. Congruent means that the polygons that you put together are all the same size and shape.

Only three regular polygons tessellate in the Euclidean plane: triangles, squares or hexagons.

Semi-regular Tessellations

You can also use a variety of regular polygons to make semi-regular tessellations. A semiregular tessellation has two properties which are:

1. It is formed by regular polygons.
2. The arrangement of polygons at every vertex point is identical.

There are the eight semi-regular tessellations.

The Muslim craftsmen in Spain in the 14th century created beautifully complex visual effects by tessellating a small simple basic tile pattern. Intricate and complex designs can be built-up from basic tile patterns in a simple way by this process.

In Tessellation planning, the creative power of tessellation is applied to town planning, where the colours are not merely decorative but represent functional space.

A small triangular tile, the mother-tile is the basic building block that creates the honeycomb layout. It contains three requisite elements of a township layout:
• road (yellow)
• House & garden (red/blue)
• Public green area (green)


Tessellate to form a courtyard of 16 houses.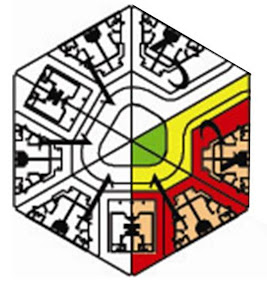



Tessellate to form three courtyards that link to become a cul-de-sac of 46 houses.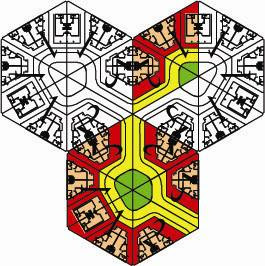




Tessellate again to form a block of about 250 houses.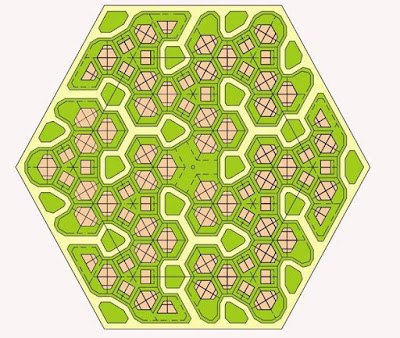



This may look complex.Like a maze. But it is only perception. In terms of geometrical construction, the pattern is simple.



Houses that link up in this tessellation form the basis of new house types. Linked Honeycomb Houses ideally joins back to back and are accessed from different cul-de-sacs. This is the case of the duplex and triplex. But they can also link side to side at the same time, as in the case of the quadruplex and sextuplex.



LAND-USE EFFICIENCY

Small-scale comparison with terrace houses

A honeycomb neighbourhood comprising 5 units of quadriplexes and duplexes is compared with a terrace house arrangement of an equivalent 5 units. Although the land size of the houses is the same, when we analyze the breakdown of land-use, we find that the area used up for roads (yellow) in the honeycomb layout is much less than that in the terrace house layout. Because we have made the green area to be of the same size, therefore there is more saleable land.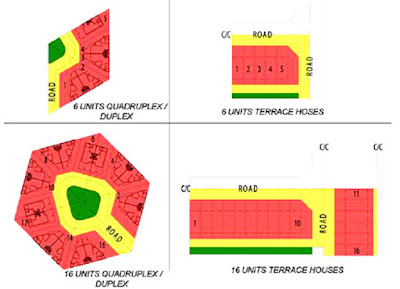




We then compared a honeycomb neighbourhood comprising 16 units of quadriplexes and duplexes against a terrace house arrangement of an equivalent 16 units. It is demonstrated in the table shown that the honeycomb layout is more land-use efficient.

A similar exercise comparing 2 and 8 detached houses laid out in rows and against the same numbers of equivalent honeycomb houses comes to the same conclusion.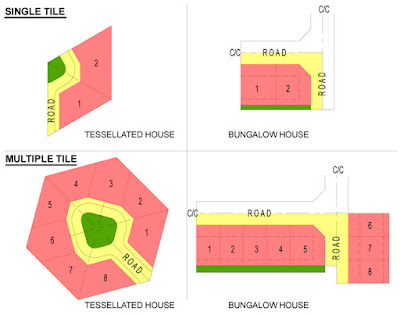




Medium-scale comparison with terrace houses

We then made a comparison between a ‘honeycomb’ layout comprising 258 three-bedroom low-medium cost double-storey houses of 1200sf built-up area on 15.6 acres of land, and that a terrace-house layout consisting of 288 equivalent 3 bedroom low-medium cost double storey houses of also 1200sf with 18’ frontage on 21.74 acres. Both layouts are efficient are theoretically efficient with the land size and shape suited to the requirements of the rectilinear and honeycomb geometry. The size of land and number of units are not exactly the same, but this is acceptable because we are interested in the ratios.


288 houses of also 1200sf on 21.74 acres

258 houses on 15.6 acres of land



We find that ‘honeycomb’ housing produces here greatly increased land use efficiencies. These advantages are summarized in the mathematical table comparing the terrace housing against quadruplex/sextuplex honeycomb housing. The density is the same but the amount of road for the ‘honeycomb’ is only 33% against 47% for the terrace. Consequently, the average size of each lot is 30% larger!



Real Site Comparisons

We have done several comparative studies, comparing actual terrace-house layouts to alternative ‘honeycomb’ layouts, to illustrate how honeycomb layouts are more efficient than conventional rectilinear grid layouts. We have done several comparative studies to illustrate how honeycomb layouts are more efficient than conventional rectilinear grid layouts. The study of alternative layouts at Demak Laut, Kuching in Sarawak is one example.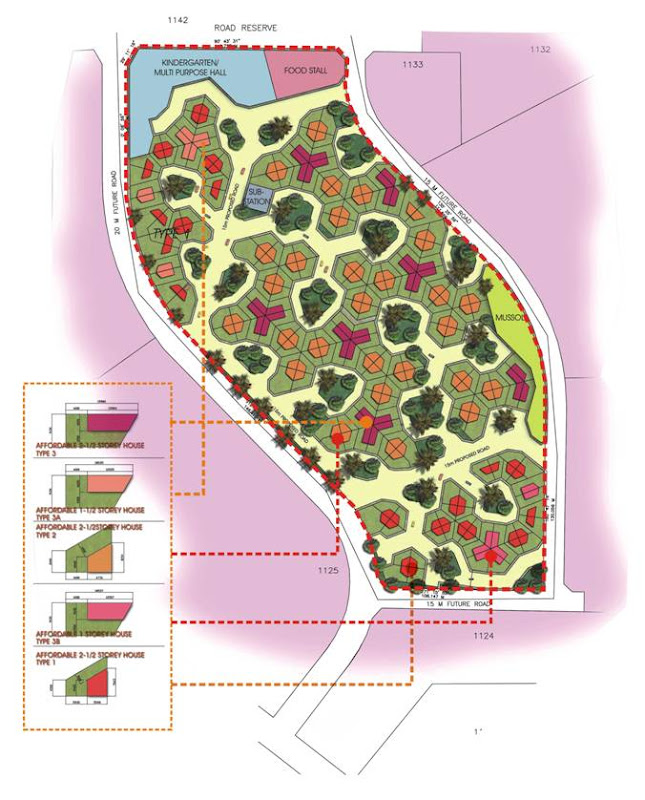




In this example, there is the same number of units. The green areas and provisions for amenities are about the same. The terrace alternative yields only about 40% sellable residential land. This yield is quite common for any landed property development. However, the honeycomb layout can yield about 56% saleable land. The reason for this can be seen in the reduction in road reserve – from 38% to 23%.





WHY IS THE HONEYCOMB LAYOUT EFFICIENT?

First of all, the back-lane in the terrace house situation is wasteful – this feature is totally eliminated in honeycomb housing.

Secondly, we can reduce the amount of circulation space in a through road by cutting it off at the end. The final length is replaced by paved area designed for turning.




Given a fixed area and number of houses to access, the shorter the cul-de-sac, the less the area taken up by the road. A square cul-de-sac neighbourhood has less road area than a long rectangular one. A circular one by itself would be the most efficient. However, as shown below the circle does not tessellate...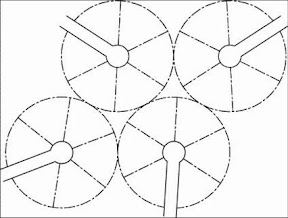





However, hexagonal neighbourhoods interlock without gap or overlap.

The third consideration is the length of the distribution roads that encircle a precinct. The perimeter of a hexagonal precinct is 7% shorter than the perimeter of a square one of the same area (figure 19).

The fourth factor is the shape of the individual lot and its effect on the buildable footprint after taking account of setback requirements. In the example shown, the truncated triangle shape of 6000 square feet yields a higher plinth area compared to a typical 60’ x 100’ site.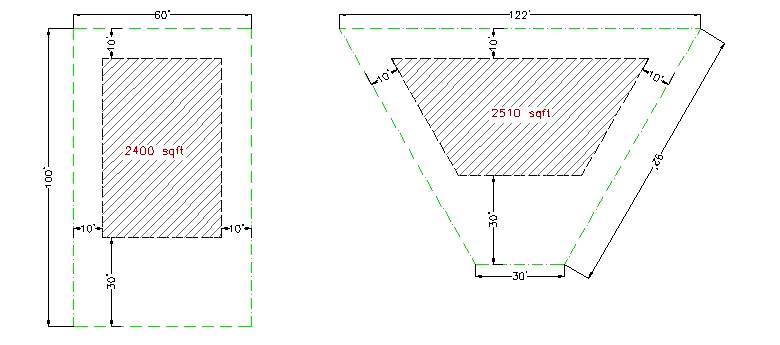



All of the above factors combine in honeycomb housing to produce greatly increased efficiency of land use. A terrace can be seen as a row of houses surrounded by roads. In contrast, honeycomb houses surround the road. It is easy to understand intuitively that roads accessing internally are more efficient than roads accessing houses from the external boundary. This accounts for the efficiency of cul-de-sacs in general, and partly explains the efficiency of ‘honeycomb housing’.

MATHEMATICAL MODEL

Distances and areas of a Tessellation Layout and an equivalent Terrace Layout were expressed in terms of variables x, y, etc.




Using formula from the Pythagoras Theorem and the Solution to Quadratic Equations, a mathematical model of the two alternatives was built up. We then track how land-use efficiency and density vary as a range of buildable footprint areas of the two alternatives are input. We were able to prove in all cases that Tessellation layouts reduce the total area of roads, thereby resulting in more saleable land, and lowering infrastructural cost. We also showed that densities can be improved.




References
Totally Tessellated website at http://library.thinkquest.org/16661/history/uses.html
Math Forum website at http://mathforum.org/sum95/suzanne/tess.intro.html